Jaringan
perpipaan merupakan merupakan suatu rangkaian pipa yang saling terhubung satu
sama lain secara hidrolis, sehingga apabila di satu pipa mengalami perubahan
debit aliran maka akan terjadi penyebaran pengaruh ke pipa-pipa lain. Perubahan
ini bisa dideteksi dari segi perubahan tekanan yang ada pada pipa.
Pipa
yang tergabung dalam suatu jaringan pipa dapat dibedakan satu dengan yang lain
dari segi :
·
Panjang pipa
·
Diameter pipa
·
Jenis pipa
·
Kedudukan pipa dalam jaringan
Kedudukan pipa dalam suatu jaringan dapat dinyatakan dengan :
·
Nomor pipa
·
Simpul atau node yang dihubungkan oleh pipa tersebut
·
Pemakaian jaringan pipa dalam bidang teknik sipil terdapat pada
sistem
Jaringan distribusi air minum.Sistem jaringan ini merupakan bagian
yang paling mahal dari suatu perusahaan air minum.Oleh karena itu harus dibuat
perencanaan yang teliti untuk mendapatkan sistem distribusi yang efisien.
Jumlah atau debit air yang disediakan tergantung pada jumlah penduduk dan macam
industri yang dilayani.
Dalam
suatu sistem jaringan air yang keluar dari node dikendalikan oleh sebuah valve
yang menghubungkan antara satu bagian jaringan dengan bagian yang
lainnya.Sedangkan secara kolektif air yang keluar dari satu node jaringan
tergantung dariperilaku konsumen. Pemakaian air sendiri secara hidrolis
tergantung dari sisa tekanan pada node tersebut sedangkan faktor lain yang
mempengaruhi adalah tingkat kebutuhan konsumen akan air.
Sebagai
asumsi misalnya 1 orang per hari memakai 200 L/org/hari, bila sebuah node
melayani 500 orang maka satu node itu mengeluarkan air sebanyak 200 L/org/hari
x 500 org = 100.000 L/hari atau 100 m3/hari atau rata-rata dalam 1
detik adalah 100.000/3600/24 = 1.1574 L atau Q = 1.1574 L/dt. Hal ini berarti
debit air keluar dari node tersebut adalah 1.1574 L/dt.
Analisis
jaringan pipa ini cukup rumit dan memerlukan perhitungan yangbesar, oleh karena
itu pemakaian komputer untuk analisis ini akan mengurangi kesulitan. Untuk
jaringan kecil, pemakaian kalkulator untuk hitungan masih dilakukan.Ada
beberapa metode untuk menyelesaikan perhitungan sistem jaringan pipa,
diantaranya adalah metode Hardy Cross dan metode matriks.
Dalam
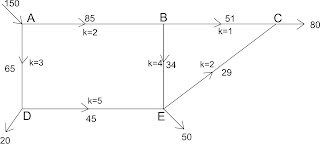
makalah ini hanya akan dibahas metode Hardy Cross. Gambar 7.6 adalah contoh
suatu sistem jaringan pipa.
| gambar sistem jaringan pipa. |
Aliran
keluar dari sistem biasanya dianggap terjadi pada titik-titik simpul.Metode
Hardy Cross ini dilakukan secara iteratif. Pada awal hitungan ditetapkan debit
aliran melalui masing-masing pipa secara sembarang. Kemudian dihitung debit
aliran di semua pipa berdasarkan nilai awl tersebut. Prosedur hitungan diulangi
lagi sampai persamaan kontinuitas di setiap titik simpul dipenuhi.
Pada
jaringan pipa harus dipenuhi persamaan kontinuitas dan tenaga yaitu :
1.
Aliran di dalam pipa harus memenuhi hokum-hukum gesekan pipa untuk
aliran dalam pipa tunggal.
Hf =
2.
Aliran masuk ke dalam
tiap-tiap simpul harus sama dengan aliran yang keluar.
∑Qi = 0
3.
Jumlah aljabar dari kehilangan tenaga dalam satu jaringan tertutup
harus sama dengan nol.
∑hf = 0
2.1.
Rumus Kehilangan Tenaga Akibat
Gesekan
Setiap
pipa dari sistem jaringan terdapat hubungan antara kehilangan tenaga dan debit.
Secara umum hubungan tersebut dinyatakan dalam bentuk :
hf = k Qm
(7.28)
Dengan
m tergantung pada rumus gesekan pipa yang digunakan, dan koefisien k tergantung
pada rumus gesekan pipa dan karakteristik pipa.Sebenarnya nilai pangkat m tidak
selalu konstan, kecuali bila pengairan berada pada keadaan hidraulis kasar,
yang sedapat mungkin dihindari.Akan tetapi karena perbedaan kecepatan pada
masing-masing pipa tidak besar, maka biasanya nilai m di anggap konstan untuk
semua pipa.Sebagai contoh untuk rumus Darcy-Weisbach.
hf = k Q2
dengan
2.2.
Metode Hardy Cross
Dianggap
bahwa karakteristik pipa dan aliran yang masuk dan
meninggalkan
jaringan pipa diketahui dan akan dihitung debit pada setiap elemen dari
jaringan tersebut. Jika tekanan pada seluruh jaringan juga dihitung, maka
tinggi tekanan pada satu titik harus diketahui. Prosedur perhitungan dengan
metode Hardy Cross adalah sebagai berikut :
1.
Pilih pembagian debit melalui tiap-tiap pipa Q0 hingga terpenuhi
syarat kontinuitas.
2.
Hitung kehilangan tenaga pada tiap pipa dengan rumus hf = kQ2.
3.
Jaringan pipa dibagi menjadi sejumlah jaring tertutup sedemikian
sehingga tiap pipa termasuk dalam paling sedikit satu jaring.
4.
Hitung jumlah kerugian tinggi tenaga sekeliling tiap-tiap jaring, yaitu hf =0.
5.
Hitung nilai ∑│2kQ│untuk tiap jaring.
6.
Pada tiap jarring diadakan koreksi debit Q supaya kehilangan
tinggi tenaga dalam jarring seimbang. Adapun koreksinya adalah
7.
Dengan debit yang telah dikoreksi sebesar Q = Q0 + Q, prosedur dari
no.1 sampai no.6 diulangi hingga akhir Q 0, dengan Q adalah debit
sebenarnya,
Q0 adalah debit dimisalkan, dan Q adalah debit koreksi.
Penurunan rumus
(7.31) adalah sebagai berikut :
= k Q02 + 2k Q0 Q + k Q2
Untuk Q <<
Q0 maka Q2 0 sehingga :
hf = k Q02
+ 2k Q0 Q
Jumlah
kehilangan tenaga dalam tiap jaringan adalah nol :
∑hf = 0
∑hf = ∑ k Q02
= Q ∑ 2kQ0 = 0
Untuk
jaringan pipa yang cukup besar hitungan dilakukan dengan komputer, tetapi untuk
jaringan kecil/sederhana dapat menggunakan kalkulator.
Hitungan
jaringan pipa sederhana dilakukan dengan membuat tabel untuk setiap jaring.
Dalam setiap jaring tersebut jumlah aljabar kehilangan tenaga adalah nol,
dengan catatan aliran searah jarum jam (ditinjau dari pusat jaringan) diberi
tanda positif, sedang yang berlawanan bertanda negatif. Untuk memudahkan
hitungan, dalam tiap jaringan selalu dimulai dengan aliran yang searah jarum
jam. Koreksi debit Q dihitung dengan rumus (7.31). Arah koreksi harus
disesuaikan dengan arah aliran. Apabila dalam satu jaring kehilangan tenaga
karena aliran searah jarum jam lebih besar dari yang berlawanan (∑k Q02>
0) maka arah koreksi debit adalah berlawanan jarum jam (negatif). Jika suatu
pipa menyusun dua jaring, maka koreksi debit Q untuk pipa tersebut terdiri
dari dua buah Q yang diperoleh dari dua jaring tersebut. Hasil hitungan yang
benar
di capai
apabila Q 0.